A BME Művészeti Rezidenciaprogram a 2023-24-es időszakra az alábbi témákra ír ki pályázatot magyar nyelven. A beadott pályázatokban meg kell jelölni, hogy a pályázó melyik témához szeretne kapcsolódni.
- Bepillantás az építőanyagok belső világába
- Fraktálok világa
- Az elfogyó káosz átmeneti bája
- Mesterséges intelligencia, zene és szerzői jog
- Részletek és összefüggések
- Anyagtan, anyagszerkezet
- Biomechanika
1. Bepillantás az építőanyagok belső világába
témavezető/mentor: Dr. Csorba Kristóf egyetemi docens, Automatizálási és Alkalmazott Informatikai Tanszék
A kutatási téma az Automatizálási és Alkalmazott Informatikai Tanszék (Villamosmérnöki és Informatikai Kar) és az Építőanyagok és Magasépítés Tanszék (Építőmérnöki Kar) közös projektje, melyben CT felvételek alapján, képfeldolgozási módszerekkel vizsgáljuk építőanyagok, elsősorban beton- és aszfaltfajták fagy- és tűzállóságát. A kutatás az építőipar számára azért fontos, mert például hagyományosan a fagyállósági teszt (sok fagyasztás és felolvasztás, heteken keresztül) nagyon sokáig tart, így ezt CT felvétellel helyettesítve nagyon sok időt nyerhetünk. Másik példa az acélszál erősítésű betonok esete: a megkötés után hagyományos módszerekkel nagyon nehéz megmondani, hogy hova is kerültek a kis, 10-15 cm hosszú acélszálak, amiket a betonba belekevertek. Az ideális az, ha egyenletesen, mindenhol jelen vannak, de előfordulhat az is, hogy keverés közben összegabalyodtak és egyetlen csomóban vannak, amitől az acélszál-erősítés szinte hatástalan lesz.
Művészeti szempontból a következő kérdések lehetnek érdekesek:
- A CT felvételekkel az építőanyagok belső struktúrájáról olyan információkat szerzünk, amire eddig ipari alkalmazásban igen kevés példa volt: a beton megkötése után a belső pórusrendszer, a különböző komponensek határfelületei, az esetleges merevítő acélszálak, tűzállóságot növelő műanyag szálak vagy más adalékok belső elrendeződéséről nem volt információ. Most mindez láthatóvá válik és az informatikai eszköztár segítségével látványos, vizuálisan is informatív formában mutatható be.
- Ugyanilyen betekintést nyerünk a leromlási folyamatokba, például a fagy- vagy tűzkár következményeibe. A belső struktúra változásai, degradálódása a fentiekhez hasonlóan vizualizálható, akár animáció formájában is.
- Az informatikai eszköztár segítségével nagyon sokféle, akár kifejezetten művészeti célú elemzést is el tudunk készíteni, mivel a szoftverfejlesztő csapat számára az nem akadály, ha valamire még nincsen kész program. Kinyerhetjük például egyetlen beton pórus 3D modelljét, a belső felületek alakját, a kavicsok egymáshoz képesti helyét. Ezekből képeket, animációkat készíthetünk, de 3D nyomtatással akár maketteket vagy öntőformákat is készíthetünk belőlük.
Már amúgy is interdiszciplináris csapatunkban a művészeti rezindenciaprogram valószínűleg sok beszélgetéssel, ötleteléssel kezdődik majd, mivel meg kell ismernünk egymás preferenciáit, céljait, valamint hogy kinek mit könnyű, mit nehéz, mit hasznos és mit felesleges megvalósítani. Ezután a művészeti alkotás elkészítéshez szükséges adatfeldolgozáshoz, információk kinyeréséhez, képek elkészítéséhez biztosítunk megfelelő szoftverfejlesztési hátteret.


2. Fraktálok világa
témavezetők/mentorok: Dr. Bárány Balázs és Dr. Molontay Roland egyetemi docensek, valamint Dr. Simon Károly egyetemi tanár, Sztochasztika Tanszék, BME Természettudományi Kar
A fraktálok olyan végtelenül töredezett, gyűrött alakzatok, amelyek kisebb részei az egészhez hasonlatos mintázatot mutatnak. Ezt nevezzük skálainvariancának. Ezen leírás Benoit Mandelbrottól származik, aki magát a fraktál kifejezést is megalkotta a latin „fractus” tört, töredezett szóból. Számos ilyen jellegű alakzat található körülöttünk, gondolhatunk csak szigetek partvonalára, kristályok növekedésére, a fák ágaira, a karfiol virágára, egy páfránylevélre, de a jelenség számos más helyen is előfordul, mint például a tőzsdei részvények véletlenszerű mozgásakor.

A fraktáloknak nincs jelenleg széles körben elfogadott precíz matematikai definíciója, de a fenti skálainvariancia tulajdonság egy explicit matematikai modelljét adják az úgynevezett iterált függvényrendszerek (IFS – iterated function system) és az általuk generált attraktorok, avagy invariáns halmazok. Tekintsünk véges sok függvényt, amelyek a síkot (vagy a teret) önmagára képezik oly módon, hogy a képpontok távolsága kisebb, mint az eredeti távolságuk. Ezeket nevezzük kontrakcióknak. A fraktálgeometria egy klasszikus tétele szerint ez a véges sok kontrakció egyértelműen meghatároz egy kompakt, nem üres halmazt, amely ezekre a függvényekre nézve invariáns. Azaz a halmaz előáll a függvényekkel vett képeinek uniójaként, ily módon téve eleget a kívánt skálainvariancának. Ezeknek a halmazoknak rendkívül érdekes matematikai tulajdonságaik vannak, méreteik és struktúrájuk a klasszikus geometria módszereivel nem megérthető. Jellemzően olyan alakzatok, melyek dimenziója nem egész szám, nem úgy, mint az egydimenziós egyenes, vagy a kétdimenziós téglalap. Nem utolsósorban rendkívül látványos formavilágot mutatnak. Kedvcsinálónak álljon itt néhány link:
IFS Construction Kit Galery
Art From Code
GitHub
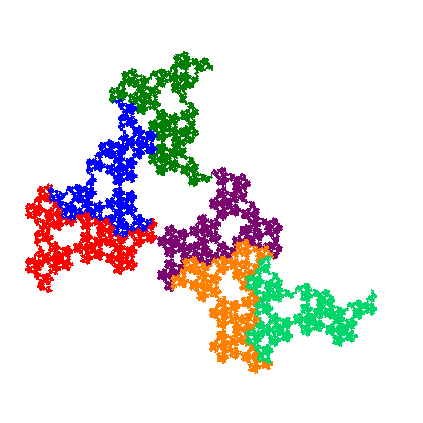
A fenti alakzatok megjelenítésének egyik módja az iterálás. Vegyünk egy alakzatot a síkon, s erre az alakzatra alkalmazzuk az IFS összes függvényét minden lehetséges sorrendben, majd vegyük az így kapott képek unióját. Az így kapott alakzat minden esetben jól közelíti az IFS invariáns halmazát. Másik módszer az úgynevezett káoszjáték, amelyben egy kiindulási pontra alkalmazzuk az IFS egy véletlenszerűen választott függvényét, majd ezt ismételjük a kapott új pontra addig, amíg a kapott ponthalmaz a kívánt közelítést el nem éri. Mindkét módszernek megvannak a maga előnyei és hátrányai egy számítógépes implementáció során. Az iterált függvényrendszereknek számos variánsa is létezik, mint az inhomogén IFS, mellyel fraktálerdők állíthatók elő, vagy a véletlen IFS, amikor az iteráció minden lépésében véletlenszerűen változtatunk az IFS függvényein, amivel fraktál-tájképek rajzolhatók. A fraktálok, köszönhetően lenyűgöző struktúrájuknak, már korábban is hatással voltak a művészvilágra, köszönhetően például Saxon Szász János-Dárdai Zsuzsa házaspár munkásságának.
A téma mentorai több éve foglalkoznak a fraktálgeometriával, s mindannyian az NKFIH Élvonal – Kutatói kiválósági Program által támogatott „Fraktálgeometria és alkalmazásai” kutatócsoport tagjai.
3. Az elfogyó káosz átmeneti bája
témavezető/mentor: Károlyi György egyetemi tanár, BME Természettudományi Kar, Nukleáris Technikai Intézet
A matematikában és a fizikában a káosz az egyszerű, jól modellezhető rendszerek szemre bonyolult, előre jelezhetetlen és megjósolhatatlan viselkedése. Hiába ismertek a rendszert leíró egyenletek, a kialakuló mozgás olyan érzékenyen függ a kezdőhelyzettől, kezdeti feltételektől, hogy azok tökéletesen pontos ismeretének hiányában nem láthatók előre a következmények. Ezt a pillangóhatás elnevezéssel szemléltetjük Edward Lorenz nyomán, akinek híres megfogalmazásában „egy pillangó egyetlen szárnycsapása a Föld egyik oldalán tornádót idézhet elő a másikon”.


Mára a dinamikai rendszerek elmélete részletesen feltérképezte a kaotikus rendszerek sajátosságait. Kevésbé lezárt terület azon esetek vizsgálata, amelyekben a kaotikus, bonyolult viselkedés csak átmeneti. Akár azért, mert a viselkedés egy idő után kilép a bonyolult lehetséges kimenetelek tartományából, akár azért, mert elfogy a kezdeti lendülete, és a mozgás lassan leáll. Mindeközben a viselkedés hosszú ideig is lehet bonyolult, és a végső, egyszerű állapota nagyon érzékenyen függ attól, hogy honnan és hogyan indult.
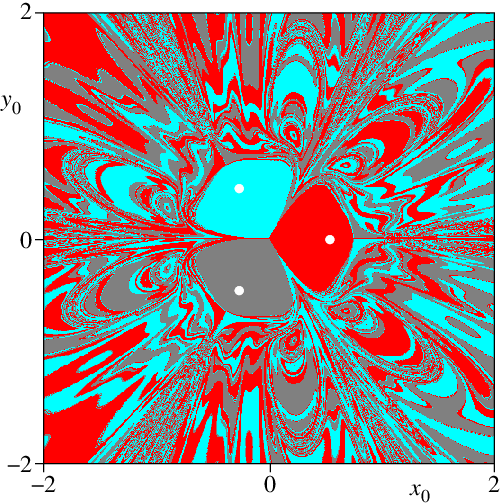
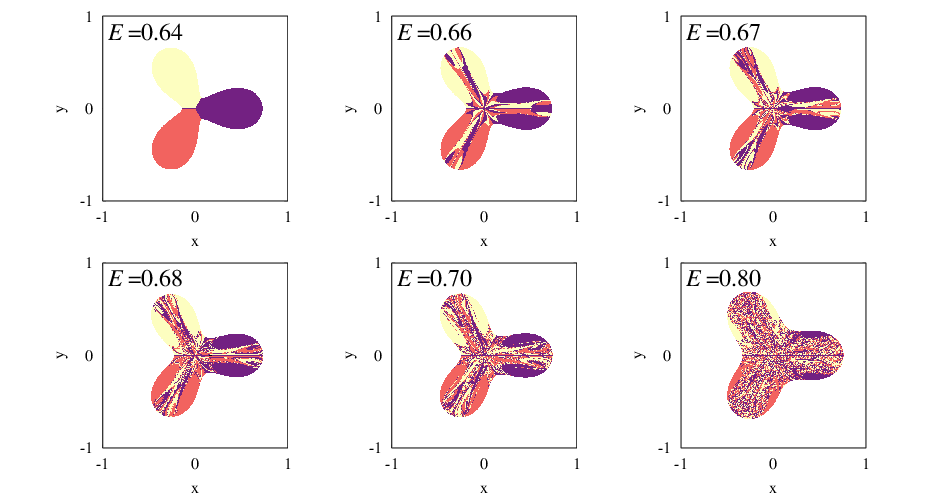
A kezdőfeltételekre való érzékenységet vizuálisan is lehet ábrázolni, ha például megfestjük a kezdeti lehetséges helyzeteket a végkimenetelre jellemző színekkel. A kapott ábrák fraktálok lesznek, amelyek a megszokottól eltérő, igen furcsa matematikai tulajdonságokkal rendelkező alakzatok. A színes fraktál alakzatokat tetszőlegesen felnagyítva az eredetihez hasonló képek bukkannak elő, bármilyen erős nagyítót is használunk. A fraktál alakzatok nem írhatók le a hagyományos geometria eszközeivel: nem bírnak egész számmal jellemezhető, törtdimenziós tulajdonságokkal.
4. Mesterséges intelligencia, zene és szerzői jog
témavezető/mentor: dr. Grad-Gyenge Anikó habilitált egyetemi docens, tanszékvezető, Üzleti jog Tanszék, dékánhelyettes, BME Gazdaság- és Társadalomtudományi Kar, és dr. Forstner Bertalan egyetemi docens, BME Villamosmérnöki és Informatikai Kar, Automatizálási és Alkalmazott Informatikai Tanszék
Mesterséges intelligencia és a szerző kapcsolata a jog szemszögéből. A szerzői jog elsődleges célja annak a szellemi teljesítménynek az anyagi és morális elismerése, amely egyéni, eredeti jellegű és éppen emiatt gazdagítja a kultúrát. A jogi szabályozás kezdetektől biztosít védelmet olyan alkotásoknak is, amelyeknek a létrehozása több-kevesebb eszköz igénybevételét teszi szükségessé. Az alkotás folyamatában korábban is voltak olyan elemek, amelyek nem az alkotó teljes kontrollja alatt születtek meg. A különböző specifikus mesterséges intelligencia eljárások alkalmazása komponálási célra új szintre emelte az eszközhasználatot és átalakította a kontroll szerepét is. Ennek az eredménye lehet, hogy az MI akár át is veheti (de mindenképp kiegészítheti) az alkotó szerepét, de még ha ez nem is következik be, a külső szemlélő, a hallgató számára ellehetetlenülhet annak a megállapítása, hogy a kompozícióban hol ér véget az alkotó és hol kezdődik a gép.
A szerző egyéni alkotótevékenységének ilyen jellegű felszámolása a szerzői jogi paradigmát is kikezdi. Az ÜJT kutatásai körében foglalkozik a szerzői jog és a technológia kapcsolatával, a MI alkalmazásának hatásaival a jogi védelem céljaira, az egyes jogintézmények fenntarthatóságára, a szerzői jog gyakorlati működésére.
Az egyik mentor kutató, Grad-Gyenge Anikó zenetudományi tanulmányok után, jogi végzettséggel immáron két évtizede foglalkozik szerzői joggal, amelyben megkülönböztetett figyelemmel kíséri a zenei szerzői jog fejlődését. Kutatási területére tartozik az MI hatása az alkotótevékenységre.
A másik mentor kutató, Forstner Bertalan maga is komoly hangszeres zenei előélettel rendelkezik, számos zenei kutatás-fejlesztési projekt részese volt már. Az egyik irány azt vizsgálja, hogyan lehet modern számítástechnikai eszközökkel a szolfézs alapokat hatékonyan oktatni (Move mi Music). A másik irány a zenei képességfejlesztés (például ritmustartási képesség) hatásának vizsgálata az egyéb kognitív területeken történő gyermekkori fejlesztésre.
A rezidens művész feladata a mentorokkal való együttműködés során olyan, mesterséges intelligenciát alkalmazó kompozíciós minták létrehozása lehet, amelyek illusztrálhatják, hogy milyen módokon tud az emberi elképzelés és a gép (MI) által javasolt zenei anyag úgy együttműködni, hogy tetten érhető legyen az egyedi szerzői koncepció, a kreatív emberi gondolat.
5. Részletek és összefüggések
témavezető/mentor: Kovács Edith Alice, egyetemi docens, tanszékvezető, Differenciálegyenletek Tanszék, Rácz Péter, egyetemi adjunktus, Kognitív Tudományi Tanszék
Guiseppe Arcimboldo festménye II. Rudolf Német-Római császárt Vertumnusként, az évszakok római isteneként ábrázolja. Ez jó példa a részletek és az összefüggések működésére. Az agyunk szeret mindenhol összefüggéseket látni (ezt hívjuk a kognitív tudományban pareidoliának). Különösen arcokat szeretünk mindenhol felismerni, akár a bárányfelhős égen, a Marson, vagy itt a festményen látható gyümölcsök között. Mégis meglepődünk, amikor észrevesszük, hogy Arcimboldo ezt az arcképet gyümölcsökből és vadvirágokból rakta ki.

Megdöbbentő lehet az, amikor megszokott részleteket más összefüggésben látunk, de az is a felfedezés frissességével hat, amikor egy problémát, amely összefüggések rendszeréből áll, úgy oldunk meg, hogy a részleteit más részletmegoldásokkal helyettesítjük. Az emberi gondolkodás a részletek és az összefüggések között egyensúlyoz. A természettudományok elvontabb módon dolgoznak a részletek és összefüggések rendszereivel. Az adattudományban például szcenárió generálási célból, kopulákat használunk a többdimenziós valószínűségi eloszlások modellezésére. Ez a függvény lehetővé teszi, hogy
külön modellezhessük a valószínűségi változók közötti összefüggéseket és a benne szereplő valószínűségi változókat.
6. Anyagtan, anyagszerkezet
témavezető/mentor: Dr. Halász György adjunktus, Építőanyagok és Magasépítés Tanszék, BME Építőmérnöki Kar
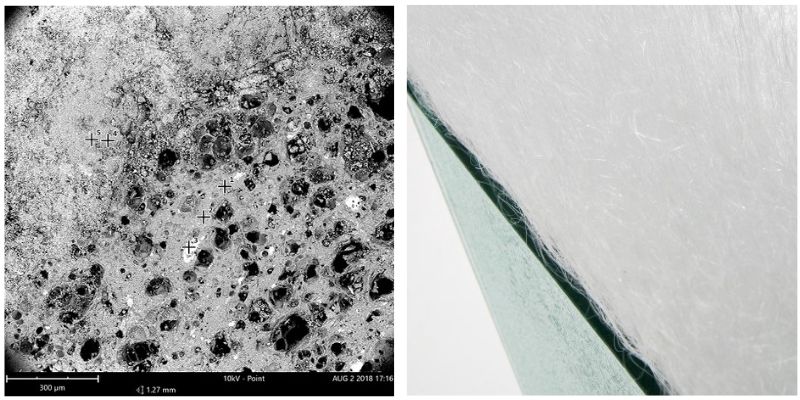
Az építőmérnök olyan foglalkozás, amely az angol Építőmérnöki Társaság 1828-as alkotmánya szerint „a természet erőforrásait az emberiség kedvére és hasznára fordítja”. Kulcsszavai: a természet ismerete; természettudományok; a környezet alakítása, formálása; az anyagok tartóssága; a biztonság megteremtése; az anyag jelként való megjelenése. Anyagtani és anyagszerkezeti kutatásainkat a tanszékünk anyagvizsgáló és épületfizikai laboratóriumai támogatják. A laborokban lehetőség nyílik különböző anyagok megismerésére és anyagminták elkészítésére. A vizsgálatok során találkozunk robosztus és monumentális anyagokkal és szerkezetekkel (pl. beton) csakúgy, mint „könnyed”, légies, transzparens építőanyagokkal (pl. üveg). Vizsgálunk természetes anyagokat (pl. szalma) és mesterséges anyagokat (pl. műanyaghabok). Kutatásainkban nemcsak makro szinten vizsgáljuk az anyagot, hanem mikro és nano szinten is, építőipari-kémiai, épületfizikai ismereteket felhasználva, azokat kibővítve. Emellett épületszerkezetek és teljes épületek tervezésével és elemzésével is foglalkozunk, ahol az anyagtudományi vizsgálatok eredményeit hasznosítjuk. Kutatásaink jelentős része foglalkozik az építőipari digitalizációval, valamint a fenntartható építőiparral, a hulladék-újrahasznosítással, a környezetkímélő építéssel, melyben a klímaváltozás hatásainak csökkentése, az alkalmazkodás és a káros hatások enyhítése is cél.

7. Biomechanika
témavezetők/mentorok: Dr. Tóth Brigitta Krisztina és Sárosiné Dr. Lakatos Ilona Éva egyetemi adjunktusok, Tartószerkezetek Mechanikája Tanszék, BME Építőmérnöki Kar
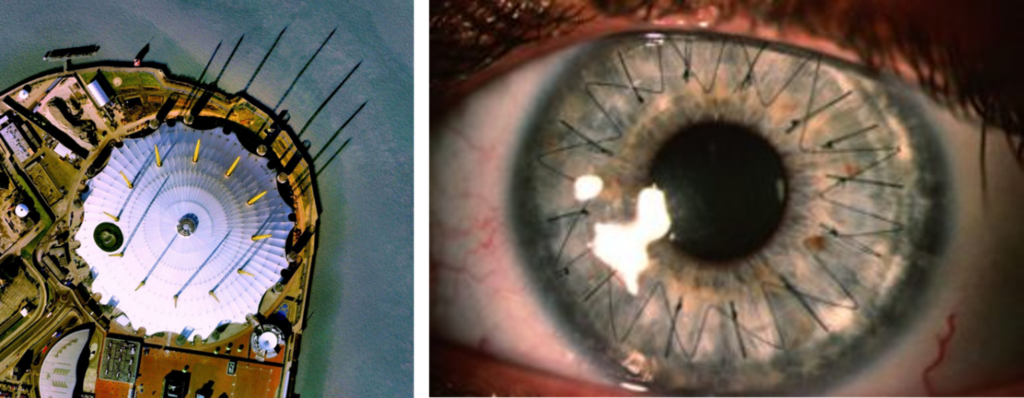
A biomechanika tudománya határterületet képez a mérnöki és orvosi tudományok között, de művelői között szép számmal vannak jelen fizikus vagy éppen biológus előképzettségű kutatók is. Páratlan szépségét épp a sokszínűsége adja. Az önmagukban is izgalmas témák (az emberi és egyéb biológiai szervezetek mechanikai szempontú vizsgálataitól vagy az érfalban áramló vér áramlásvizsgálataitól egy ízületi protézis megtervezéséig vagy az ínak nyújtásának sejtszintű leírásáig) összehozzák és közös gondolkodásra inspirálják a különböző területekről érkező szakembereket, miközben elengedhetetlen segítséget nyújtanak egyes orvosi beavatkozások megtervezésében, gyógyulási folyamatok elősegítésében vagy éppen egy szerv vagy szervrendszer működésének mélyebb megismerésében. A biomechanikai kutatók munkáját kísérletes vizsgálati módszerek, laboratóriumi mérések, valamint számítógépes szimulációk is segítik.
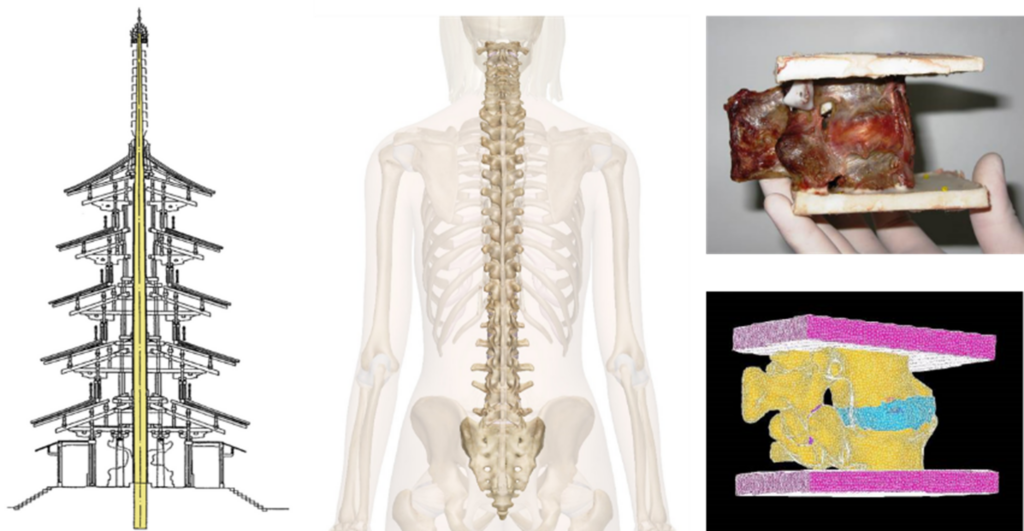

A biomechanikát az emberi test és más biológiai szervezetek mérnöki szempontú megközelítése és a különböző kutatói irányzatok együttműködéséből fakadó sokszínűsége izgalmas és inspiráló témává teheti bármely művészeti ág művészei számára.
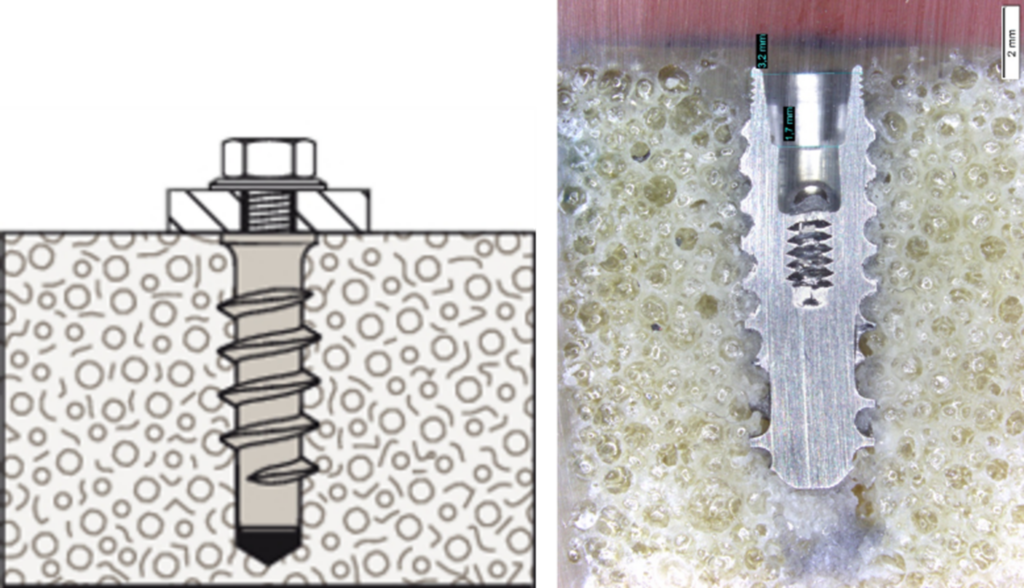
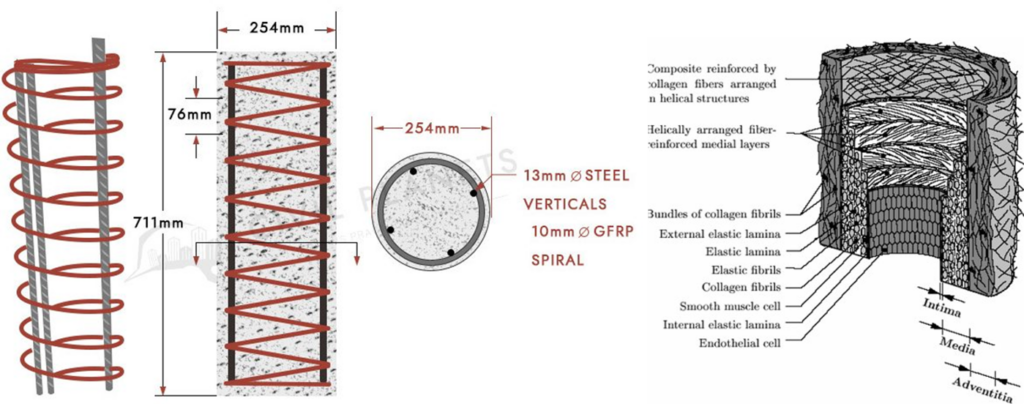
A téma mentorai mindketten építőmérnök és egészségügyi mérnök hátterű, de legaktívabban biomechanikával foglalkozó kutatónők. A biológiai anyagok iránti szeretetük összefonódik a természet ihlette mérnöki szerkezetek iránti rajongásukkal. A természet formái megihletnek művészt, mérnököt egyaránt. A mechanikailag jól működő szerkezet a szemnek is szép.
A 2023-ban meghirdetett magyar nyelvű pályázati kiírás portálunkon elérhető.


