Artists applying for the 2024 Spring residency should pick one of the following topics and indicate their choice in their motivation letter.
1) The World of Fractals
Mentors: Dr. Balázs Bárány (balubs@math.bme.hu), Dr. Roland Molontay (molontay@math.bme.hu) (associate professors), and Dr. Károly Simon (simonk@math.bme.hu) (professor), Department of Stochastics, BME Faculty of Natural Sciences
Fractals are fragmented geometric shapes, which consist of smaller parts, each pattern individually resembling the whole. This phenomenon is called scale invariance. This description was given by Benoit Mandelbrot, who invented the term „fractal” based on the Latin fractus, meaning „broken” or „fractured”. These types of patterns can be found all around us – like the coastlines of islands, the growth of crystals, the branches of trees, the cauliflower, and even in the random movement of stock market shares.

There is no widely accepted mathematical definition of fractals, but the so-called iterated function systems (IFS) and their attractors give an explicit mathematical model for the scale invariance property. For example, let us consider a finite number of functions which map 2D (or 3D) space onto itself in such a way that the distances between mapped points are smaller than their original distance. A classical theorem of fractal geometry states that such a finite collection of contractions uniquely determines a non-empty compact set (called the attractor), which is invariant with respect to the functions. That is, the attractor is equal to the finite union of its images by the functions of the IFS, and so, it has the scale invariance property. These objects have very interesting mathematical properties, and their size and structure cannot be understood by the methods of classical geometry. These shapes typically have a non-integer value dimension, unlike intervals, which are one dimensional; or squares, which are two dimensional. Last but not least, their visual representation is spectacular. To showcase some examples:
https://larryriddle.agnesscott.org/ifskit/gallery/gallery.htm
https://art-from-code.netlify.app/day-2/session-1/
https://github.com/zephyrtronium/xirho
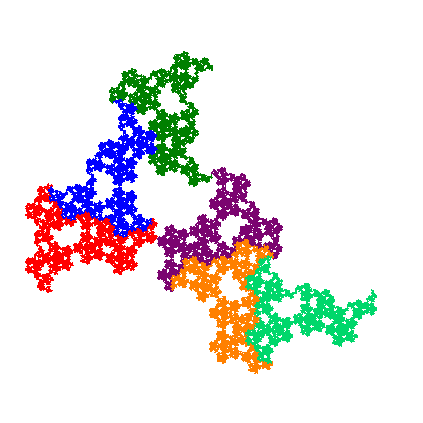
One way to plot these objects is iteration. Let us consider an arbitrary bounded domain on the plane, and then let us apply all of the possible functions of the IFS in all of the possible sequences and take the union of these images. Let us repeat this procedure again and again. This sequence of shapes will adequately mimic the IFS. Another way is the so-called chaos game. Taking an arbitrary initial point on the plane and applying a randomly chosen function of the IFS on it – then repeating the procedure on the new points until the resulting set of points reaches the desired approximation. Both methods have their advantages and disadvantages during a computer implementation. There are several versions of the iterated function systems, like the inhomogeneous IFS, which are capable to plot fractal forests, or the random IFS, when during the iteration we modify the functions of the IFS randomly, and which can plot fractal landscapes. Fractals, thanks to their impressive structure, have already influenced the art world, thanks to the work of the couple János Saxon Szász-Zsuzsa Dárdai, for example.
The mentors of the topic have been working on the field of fractal geometry for several years, and they are all members of the „Fractal geometry and applications” research group supported by the NKFIH Élvonal – Research Excellence Program.
2) Movement and Art
Mentors: Dr. Rita Mária Kiss, professor, Head of Dept. and Dorottya Ágoston Phd student, Dept. of Mechatronics, Optics and Mechanical Engineering Informatics
Movement is a form of art: just think of ballet, dance, or a figure skating exercise. How many times have we exclaim when we witness such movements: How spectacular! And of course, at the same time, we often argue, whether we liked them, or not. The aim of the measurements carried out in the Motion Laboratory of the BME Faculty of Mechanical Engineering, Department of Mechatronics, Optics and Mechanical Informatics is to characterize each movement with numbers. The numerical description of the movement helps to compare different type of motion and to find the optimal sports movement. This can help to physicians in establishing a diagnosis and determining the effectiveness of rehabilitation – and it can also help painters and photographers create the ideal setting. Perhaps we can find the optimal range for the most beautiful pirouette. But motion analysis is also a game: think of video games, or the modern ABBA concert personified by avatars. What would happen if a classical concerto was performed not by two artists, but instead by an artist and an avatar? Our laboratory the perfect place to conduct the necessary measurements.
3) Beauty of Flows
Mentors: Dr. György Paál full professor, head of department; Sára Till assistant professor, Dept. of Hydrodynamic Systems
The department specialises in applied fluid mechanics. Fluid mechanics is the science of moving liquids and gases, with applications ranging from the medicine of the vascular system to constructing pipe networks, to building pipe organs. Flows are beautiful, hence there is a competition for the most beautiful visualisations at many fluid mechanics conferences. Flows have their own rhythm; they are closely related to sound and music. They have unique internal structures, which we try to explore by a variety of tools. Flows tell stories.
4) Details and Context
Mentors: Edith Alice Kovács (kovacsea@math.bme.hu), Associate Professor, Head of Department, Department of Differential Equations, Péter Rácz (racz.peter.marton_at_ttk.bme.hu), Assistant Professor, Department of Cognitive Science
Guiseppe Arcimboldo’s painting depicts the Holy Roman Emperor Rudolf II as Vertumnus, the Roman god of the seasons. It is a good example of the interplay of detail and context. Our brains like to find connections everywhere (we call this pareidolia in cognitive science). In particular, we recognise faces all over the place: in the clouds, the sky, on the surface of Mars, or among the fruits in this painting. We are still surprised when we notice that Arcimboldo constructed this portrait out of fruits and wildflowers.

It can be shocking to see familiar details in a different context, but it also also gives us a fresh sense of discovery when we solve a problem that is a system of interconnections by replacing some of its details with others. In data science, for example, we use copulas to model multivariate probability distributions for scenario generation. These functions allow us to separately model the dependency structure between random variables and the probability distribution of the random variables involved.
5) Biomechanics
Mentors: Dr. Brigitta Tóth (toth.brigitta@emk.bme.hu) and Dr. Éva Lakatos (lakatos.eva@emk.bme.hu), Associate Professors, Department of Structural Mechanics, Faculty of Civil Engineering, BME
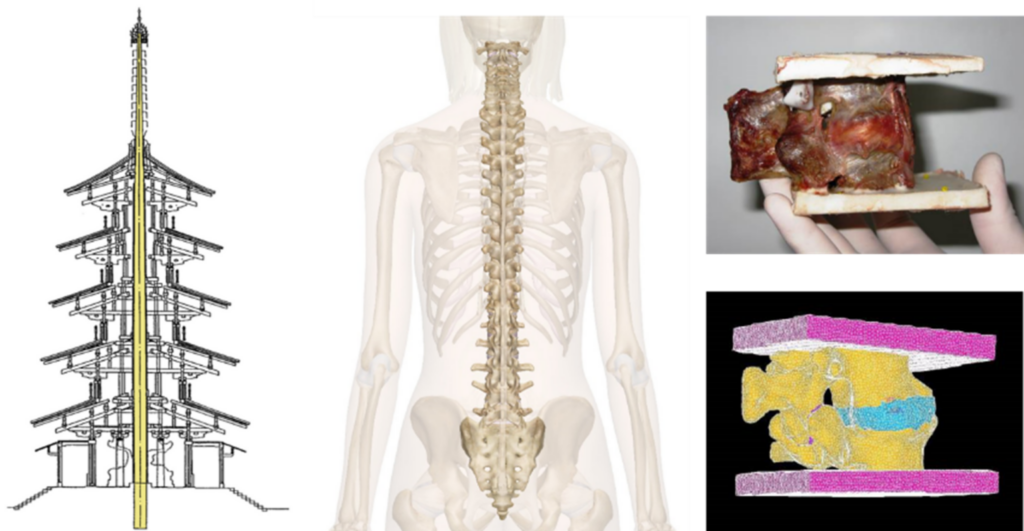
The science of biomechanics is at the frontier between engineering and medical sciences, but its practitioners include a large number of researchers with a background in physics or biology. Its unique beauty lies in its diversity. The topics are fascinating in themselves (from the mechanical aspects of human and other biological organisms, or the study of blood flow in the vascular wall, to the design of a joint prosthesis or the cellular description of the stretching of a tendon), bringing together and inspiring specialists from different fields to think together. It is also valuable in helping to plan medical interventions, to facilitate healing processes or to gain a deeper understanding of the functioning of an organ or organ system. The work of biomechanics researchers is aided by experimental methods, laboratory measurements and computer simulations.


